Overtonerekka er kanskje den koblingen mellom musikk og matematikk jeg finner vakrest av alle. Overtoner finnes i praktisk talt alle naturligskapte toner, og selv om et utrent øre ikke hører dem, vil vi alle merke godt den dagen de forsvinner. Jeg velger å ta for meg overtonerekka såpass tidlig i oppgaven, da jeg ser på den som en slags “objektiv forklaring” på en del subjektive fenomener, som opplevelsen av konsonans/dissonans.
Jeg lærte selv først om overtoner/overtonerekka i det daværende musikkfaget “musikklære/hørelære/lytting” på videregående, og har selv undervist overtonerekka i det nåværende faget “lytting”. Derfor er det her jeg vil ta utgangspunkt for å forsvare dette kapittelet. Lyttefaget er et 1.klasse fag, og det ikke et stort fag. Totalt består det av 56 klokketimer (Internettkilde 5: timetall). Med kunnskapsløftet finnes det strengt talt ikke noe som heter pensum lenger, bare kompetansemål. Lærere står friere enn tidligere til å velge hva faget skal inneholde, og følgelig vil jeg ikke finne noe sted i læreplanen hvor det står at elevene skal lære overtoner. Så jeg må finne noe som tilsier at dette er naturlig å lære dem.
Fagets hovedelementer er “musikkforståelse” og “musikkens elementer” (Internettkilde 5: hovedområder), og det er særlig i musikkens elementer vi kan forsvare overtonene. Om musikkens elementer står det at “Hovedområdet dreier seg om gjenkjennelse og beskrivelse av musikkens grunnelementer, med utgangspunkt i aktiv lytting og noteforståelse (ibid: hovedområder).” Kompetansemålet knyttet til musikkens elementer er følgende: “gjenkjenne og beskrive musikkens grunnleggende elementer med utgangspunkt i klingende musikk og enkle notebilder(internettkilde5: Kompetansemål).”
At overtonerekka er et grunnelement i musikken er for meg hevet over en hver tvil. Den finnes i alle toner, og følgelig i all musikk. Spørsmålet om det er naturlig å undervise det her er derimot kanskje ikke så entydig. Det kan argumenteres for at elementer som melodi, rytme, form og instrumentkunnskap er viktigere, da dette er ting elevene kanskje får mer bruk for i det daglige. Imidlertid mener jeg at det ikke er unaturlig å gi overtonene sin avdeling. Som jeg skal vise i dette kapittelet finnes det musikk som er komponert med overtoner som utgangspunkt og de er helt grunnleggende for alle messingblåsere. Uten overtonerekka ville antall toner du fikk ut av en trompet vært begrenset.
Frekvens og tonehøyde (Åpningen her må redigeres ordentlig)
Før jeg tar for meg overtonerekka, føler jeg det er nødvendig med et lite blikk på oppbygning av hva en tone er, og hvordan vi oppfatter den. For en grundigere gjennomgang av dette anbefaler jeg f.eks Garreth Loy (2006) sin bok Musimathics, eller Sir James Jeans (1968)sin bok Science & Music. Jeg kommer ikke til å gjøre en komplett gjennomgang av lydens oppbygning, men fokusere på det jeg mener er nødvendig med tanke på overtonerekka.
Rent fysisk er lyd trykkvariasjoner som sprer seg gjennom et materiale (for eksempel luft), og som registreres og oppfattes av øret. Vi snakker gjerne om lydbølger som disse variasjonene, og disse lydbølgene blir ofte fremstilt på denne måten: 
Grafens høydepunkt viser det høyeste trykket, mens grafens bunnpunkt det laveste. Den vannrette linja i midten er normaltrykket. Hvor stort utslag bølgene har kalles amplitude, og oppfattes som variasjon i lydens styrkegrad. Bølgenes hyppighet kalles frekvens, og oppfattes som variasjon i lydens tonehøyde.
I vår sammenheng er det frekvens som er mest interessant. Garreth Loy (2006: 13) beskriver frekvens som en fysisk måleenhet av vibrasjoner per sekund. Mens “Pitch” eller tonehøyde er den tilsvarende sanseerfaringen av vibrasjonene. Altså er det her snakk om 2 sider av samme sak. På den ene siden har vi de rent fysiske lydbølgene og en måleenhet for antall svingninger per sekund. På den andre siden har vi vår opplevelse av disse svingningene. For eksempel oppleves 440 svingninger per sekund (440hz) som 1strøken a for oss.
Pytagoreerne viste at avstanden mellom 2 toner kan uttrykkes ved et tallforhold. Vi opplever f.eks kvintintervallet som en konstant størrelse. Enten det er mellom 2 dype toner, eller to lyse toner vil vi oppleve avstanden som lik. Dette forteller oss derimot ikke noe som helst om frekvensdifferansen mellom disse 2 tonene. Hvis jeg f.eks sier at jeg har to toner som ligger med en avstand på 220hz, kan dette oppleves som en oktav (mellom a og a1), en kvint (a1 og e2) eller en stor ters (a2 og c#3) bare for å nevne noen eksempler. Hadde jeg derimot sagt at den lyseste tonen har en frekvens 1,5 ganger så høy som den laveste tonen, altså har forholdet 3:2, ville tonene klingt som en kvint uavhengig av hvor lys/mørk tonen er lagt.
Dette forholdet mellom frekvens og tonehøyde er viktig å være seg bevisst når man blant annet jobber med overtonerekka. 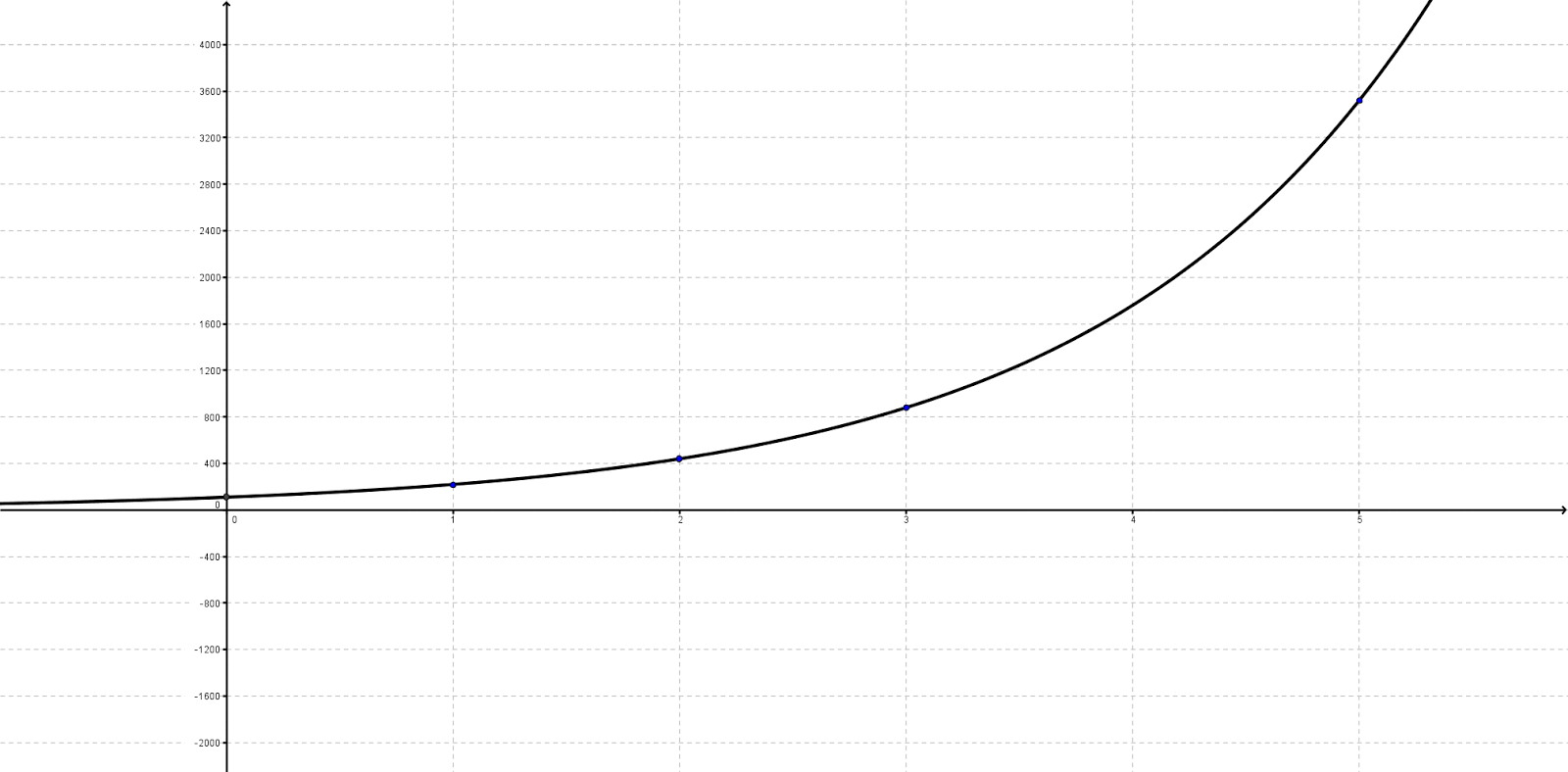
Denne grafen viser hvordan frekvensen øker, hvis opplevd tonehøyde stiger jevnt. Et skritt på x-aksen tilsvarer en opplevd tonehøydeøkning på en oktav, mens y-aksen viser tilhørende frekvens. Grunntonen jeg har tatt utgangspunkt i her er store A (110hz), og formelen for å beskrive denne grafen er y=110*2^x. Frekvensen vil øke eksponentielt hvis opplevd tonehøyde skal stige jevnt.
Hvis vi snur rundt på denne grafen, og vil la frekvensen øke konsant og se på hvordan opplevd tonehøyde varierer får vi denne grafen: 
Jeg har tatt utgangspunkt i samme formel som i forrige bilde, men omformet den slik at x-aksen og y-aksen i praksis har byttet plass. Formelen som beskriver denne er y= ln(x/110)/ln2.
Her øker frekvensen med 110 per merket enhet på x-aksen, mens opplevd tonehøyde øker med en oktav for hver enhet på y-aksen. Som vi ser stiger opplevd tonehøyde saktere og saktere. Denne grafen kan tolkes som en grafisk fremstilling av overtonerekka. Hvert markert punkt på grafen tilsvarer en overtone i overtonerekka til store A (110hz).
Overtonerekka. Hva er den?
Overtonerekka finnes i all vår musikk. Enten det er snakk om en korkonsert, eller topp 20 på radioen vil overtonerekka være representert. Det vi opplever som en naturligskapt tone består i virkeligheten av mange toner/svingninger som klinger sammen. Disse medklingene tonene ligger lysere enn den grunnfrekvensen vi oppfatter, og kalles overtoner. Andre begreper som beskriver det samme er partialtoner og naturtoner. Selv om de beskriver det samme, sier hvert av ordene noe esensielt. Overtoner forteller oss at disse ekstratonene klinger over (lysere enn) grunnfrekvensen. Partialtoner forteller oss at disse tonene er en del (part) av en helhet. I matematikken snakker man om sammensatte tall og primtall. F.eks kan tallet 100 faktoriseres til 2*2*5*5. 100 er et sammensatt tall som består av faktorene (delene) 2*2*5*5. På samme måte er hver partialtone en del av den tonen vi hører, selv om vi ikke er disse delene bevisst. I ordet naturtoner ligger det at disse tonene finnes i naturen. Det er ikke noe mennesker har “funnet opp”. I en hver naturskapte tone klinger disse med om så i forskjellig styrkegrad. Overtonerekka har eksistert fra tidenes morgen, men ble først oppdaget på 1500tallet av Marin Mersenne(1588-1648). Fenomenets matematiske lovmessighet først klarlagt i 1701 av Joseph Sauveur (1653-1716) (Sundberg 2007: 24-27).
Garreth Loy (2006: 29), skiller mellom instrumenter med “harmonic partials” og “inharmonic partials”. I første gruppe har vi instrumenter som fløyte, fiolin. Kort sagt har alle “melodiske instrumenter”. Instrumenter som trommer, og bjeller har uharmoniske overtoner (ibid: 29). De har heller ikke klart definert tonehøyde. Selv om vi hører en tydelig frekvensforskjell, mellom en basstromme og en liten tam, er det vanskelig å definere noe tydelig tonehøyde.
Overtonerekka tilhører instrumentene med “harmonic partials”. Overtonene til et melodisk instrument er heltallige positive multiplum av grunnfrekvensen (Loy: 2006: 29). Dette betyr at hvis vi har en grunnfrekvens F. Vil overtonene ha frekvensene 2F, 3F, 4F, 5F osv. F. eks. kan vi bruke store A som eksempel fra forrige delkapittel. Store A har frekvensen 110hz, og dens overtoner vil følgelig ha frekvensen 2*110hz=220hz, 3*110h=330hz 4*110hz=440hz osv.
Frekvensen øker altså konstant for hver nye overtone i overtonerekka, og som vi så av figur xx, betyr dette at opplevd tonehøyde kommer tettere og tettere.
Følgende bilde viser overtonerekka til store C:
Som vi ser av overtonerekka kommer overtonene tettere og tettere fordi forholdet mellom 2 påfølegnde overtoner blir likere og likere. F.eks er det en kvart mellom 3 og fjerde overtone (3:4), mens 5 og 6 overtone har avstand på en liten ters (5:6). I teorien har ikke overtonerekka noen begrensning og overtonene vil komme tettere og tettere mot en grenseverdi på 1:1, altså 2 like toner. I praksis er det vanskelig å notere overtoner over nr. 16 i vårt notesystem fordi de da begynner å ligge tettere enn halvtonen.
En interessant observasjon er at de intervallene som pytagoreerne regnet som de konsonerende, er de 3 første intervallene vi finner i overtonerekka, og de eneste intervallene som finnes i løpet av de 2 første oktavene (se mer om dette i kapittel xx). Man kan argumentere med at det var pytagoreernes subjektive oppfatning at disse intervallene låt renest, men at de er de første intervallene i overtonerekka er et faktum. En objektiv sannhet som kan forsvare pytagoreernes observasjon.
En annen ting jeg syns er interessant å observere er at for hver nye oktav i overtonerekka dobles antall overtoner. 1 oktav inneholder kun grunnfrekvensen, mens 2 oktav inneholder oktaven og kvinten over osv.
Overtonenes praktiske betydning
Overtonerekka er som seg interessant å studere. Men hvis den ikke hadde hatt noen praktisk betydning, ville det virke fjern å undervise om den på videregående. Jeg vil i dette kapittelet se på noen av de praktiske sidene ved overtonerekka.
Klangfarge
Klangfargen (timbre) til en tone er et av de feltene overtonenes eksistens kan oppleves i praksis. Å definere klangfarge kan være vanskelig. Garreth Loy (2006: 28) skriver blant annet at klangfarge brukes “in a general sense to describe an instrument’s sound quality as sharp, dull, shrill and so forth.” Han skriver videre at en lett mate å forklare klangfarge er å si noe om hva det ikke er. “timbre is everything about a tone that is not its pich, not its duriation, and not its loudness (ibid: 28).” Som Loyd påpeker er slike negative definisjoner ikke uten problemer. Imidlertid føler jeg at det får frem et viktig poeng. Hvis vi hører en fiolin og et piano spille samme tone, med samme styrkegrad og samme lengde hører vi fortsatt en tydelig forskjell. Hvordan man beskriver denne forskjellen er kanskje individuell, men at det er noe mer til en tone enn lengde, styrke og tonehøyde er tydelig.
Og årsaken til denne forskjellen ligger i overtonene. Hadde man fjernet alle overtonene fra pianoets og fiolinens tone, hadde forskjellen mellom dem vært borte (Og ingen av dem hadde hatt sin karakter). Overtonerekka er i utgangspunktet den samme for alle melodiske instrumenter, men det er ulikt fra instrument til instrument hvilke overtoner som klinger med, og styrkeforholdet mellom dem. Blant annet har blåseinstrumenter med rør som er tett i en ende, kun “oddetallsovertoner”(Loy 2006: 264-265). Dvs kun frekvenser som er et oddetall ganger grunnfrekvens (1F, 3F, 5F osv..). Klarinetten er et eksempel på dette (Ibid: 264-265). Styrkeforholdet mellom overtonene er det som gir instrumenter forskjellig klangfarge (Raude 2000: Kap 2.3). Dette gjelder forøvrig ikke bare fra instrument til instrument, men også samme instrument utfra hvordan spiller på det (ibid). Et hard anslag på piano vil gi en annen klang enn et mykt anslag, og hvilken munnstilling man har vil påvirke klangfargen i en saksofon.
Messinginstrumenter
Et spørsmål jeg stilte meg på videregående var: Hvordan kan en trompet spille kromatisk over 3-oktaver+ med bare 3 knotter. Med enkel kombinatorikk kan vi regne ut at 3 knotter gir totalt 8 mulige kombinasjoner for hvordan disse knottene kan være trykket ned eller ikke. Logisk sett må det da være slik at det kan spilles flere toner per kombinasjon. Knottene til en trompet fungerer på følgende måte. den ene senker grunntonen med et halvt trinn, den andre med et helt trinn og den tredje med halvannet trinn. Totalt sett kan man altså senke tonen kromatisk fra 0 til 3 hele trinn (tritonus), og vi har i praksis 7 forskjellige grunnfrekvenser en trompet kan operere med. Hver av disse grunnfrekvensene har sin tilhørende overtonerekke, og disse overtonene kan man ved hjelp av hvordan man blåser frembringe. Altså kan man få en av overtonene til å klinge istedet for grunnfrekvensen. Den dypeste normale tonen for en trompet er enstrøken c (bb natura) på instrumentet. Dette er imidlertid den første overtonen i overtonerekka til lille c (Bb natura). Neste tonen man får med åpent grep er følgelig enstrøken g, så 2strøken c osv. Følgende bilde viser de første overtonene til de forskjellige grepene på trompeten:
Alle disse tonene kan en trompet spille ved de forskjellige grepene. Vi ser at summen blir en kromatisk skala. Det er også verdt å merke seg at de dypeste tonene finner vi bare i en av rekkene. Første tone jeg finner minst 2 steder er 1strøken f#. Dette forteller at for å kunne få en kromatisk rekke helt fra starten av trenger vi minst 3 ventiler, og muligheten til å variere grunnfrekvensen innen en tritonus. La oss anta for moroskyld at trompeten kun har 2 ventiler, og mulighet til å senke grunnfrekvensen med halvannet trinn. I såfall faller de tre nederste rekkene bort, og vi har bare intervallet c1-a å operere med. Nå vil det være først fra tonen a, at instrumentet kan spille kromatisk. Men sett fra en annen side jo lysere vi kommer jo flere kombinasjoner finnes det for hver enkelt tone. I gammel tid hadde ikke messinginstrumentene ventiler, og var begrenset til en enkel overtonerekke. Det finnes fortsatt instrumenter som er begrenset av overtonerekka. Seljefløyte er et eksempel på dette.
Differansetoner. Virtuell grunntone
Differansetoner ble i følge Sir James Jeans (1968: 237) oppdaget i 1745 av den tyske organisten Sorge, og uavhengig av Tartini i 1754. Dette fenomenet er kanskje det som i sterkest grad viser overtonenes betydning i vår hverdag. Albregtsen og Skagestein (2007: 125). skriver følgende: “Hvis hjernen synes at det ‘burde være’ en grunntone på en viss frekvens, vil vi kunne oppfatte en grunntone selv om det ikke finnes noen.” Dette betyr i praksis at hvis vi tar opp en (sammensatt) tone, og digitalt fjerner grunnfrekvensen, men lar overtonene klinge, vil vi fortsatt oppfatte grunnfrekvensen. Albregtsen og Skagestein (2007:125) viser som eksempel at hvis man lar 3 toner med frekvensen 200hz, 300hz og 400hz klinge sammen, vil vi oppfatte en virtuell grunntone på 100hz. Rent generelt kan vi si at om flere frekvenser klinger sammen, kan vi oppfatte en grunnfrekvens som ligger på disse frekvensenes største felles divisor. I vårt eksempel er 100 det største tallet som både 200, 300 og 400 kan deles på for å få et heltallig svar. Musikalsk sett betyr hvis flere toner klinger sammen, vil den lyseste tonen som har alle disse tonene i sin overtonerekke klinge med. Hvis for eksempel tonene a1(440hz) , c#2(550hz) og e2 (660hz) klinger sammen, vil vi kunne de skape grunnfrekvensen store A (110hz), siden det er den lyseste tonen som har alle disse tonene i sin overtonerekka.
En ting er hvordan dette kan gjøres eksperimentelt ved å manipulere lyd. Et annet spørsmål er hvor stor betydning dette har i praktisk musikkbruk. Selv skal jeg innrømme at jeg ikke oppfatter disse differansetonene til vanlig når jeg synger og spiller. Men jeg tenker heller ikke noe større over overtonenes eksistens. I følge Sir James Jeans (1968:237) kan de høres ganske tydelig hvis man spiller to tilfeldige toner i Kvintavstand. Førsteinntrykket er kanskje at differansetoner er en forstyrrende for oss. Imidlertid har jeg til gode å høre folk klage på dette fenomenet, og det er noen praktiske fordeler med dette også.
Et eksempel er toner som ligger på grensen til hva vi kan høre i dybden. Albregtsen og Skagestein (2007:125) bruker de dypeste tonene på pianoet som et eksempel. Disse ligger i det aller dypeste registeret at hva menneskets øre kan oppfatte, og vi er veldig lite fintfølende på så dype frekvenser. Imidlertid hører vi de dypeste tonene på pianoet godt. Forklaringen ligger i overtonene. Selv om vi ikke hører selve grunntonen godt, ligger overtonene i et register vi hører utmerket og grunntonen oppfattes som sterk (Ibid: 125).
Sir James Jeans (1968: 240-241) viser et annet interessant eksempel, nemlig telefonen. Han skriver at høytaleren i en god moderne telefon (i 1937) kan dekke frekvensene mellom ca 300hz og 2400hz. Frekvenser innen dette området høres klart, mens lysere og dypere frekvenser oppfattes nesten ikke. Den vanlige snakkestemmen til både damer og menn ligger dypere enn dette frekvensområdet, og følgelig er det veldig lite grunnfrekvenser som blir formidlet gjennom telefonen. Derimot høres overtonene tydelig, og hjernen “rekonstruerer” det riktige lydbildet utfra disse (ibid: 241).
Overtonerekka brukes også aktivt i komposisjoner. Jeg skal vise dette ved et eksempel senere. Et mer generelt eksempel er 1900tallets spektralmusikk komposisjonen er informert av overtonespekteret til lyder (Griffiths 2010: 339). Forståelse av overtonene var også avgjørende i den elektroniske musikken. Når f.eks Stockhausen brukte elektronisk lyd for å lage klanger som aldri hadde eksistert før, var det gjennom å kontrollere hver enkelt deltones tonehøyde og volum (Rudi 2008: 15-16). Midilyder som etterligner akustiske instrumenter, er også basert på akkurat samme prinsippet. Elektronisk musikk er et interessant fenomen gjennomsyret av matematikk. Imidlertid er det ikke tema for denne oppgaven.
Ingen kommentarer:
Legg inn en kommentar